Federico ZanetelloのTwitterアカウント:@zntfdr
更新:この記事のフォローアップはこちらです。
グラフ理論という言葉を聞いたことがある人は、ダイクストラ法アルゴリズムについても知っているはずです。
もし聞いたことがなかったとしても、大丈夫!この記事には、知っておくべきすべてのことが掲載されています。
簡単な紹介
この章では、グラフ理論とダイクストラ法アルゴリズムがどのようなものかを説明します。
知識に自信がある方は、この章を読み飛ばしてください!(「Swiftのお時間です!」の章までジャンプしてください!)
グラフ理論
記事の最初に載っていた画像を見ましたか?これは、グラフと呼ばれる数学とコンピュータサイエンスの分野における理論です。
丸はノード(または頂点)と呼ばれ、グラフのエンティティ(実体)を表します(詳細は後述します)。ノードを結ぶ線をコネクション(またはエッジ)と呼びます。
常に2つのノードを連結するこれらのコネクションには、主に双方向と単方向の2種類があります。
双方向は、コネクションが両方向で機能すること(当たり前ですよね!)を意味します。一方、単方向は、あるノードから他のノードへのコネクションのみが存在する(その逆はない)ことを意味します(逆方向の連結には2個目のコネクションが必要です)。
これらのシンプルなコンセプトは、世界中で幅広く応用されており、あなたはおそらく常に使用しているはずです!
実世界での使用例
双方向グラフ:Facebook
あなたのFacebookの友人のグラフを可視化してみましょう!
こんな感じで示すことができます:
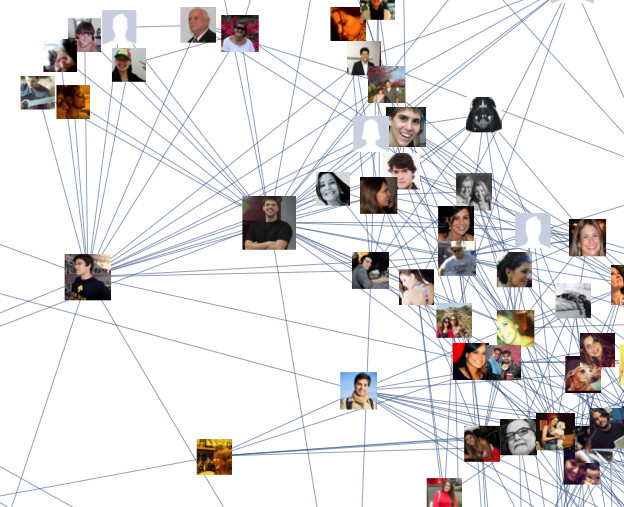
Mathematica StackExchangeから引用した画像
このグラフでは、各ノードは個人であり、各(双方向)コネクションはこれらの人々の間の友人関係を表しています。
「偶然にも」Facebookの開発者向けAPIはGraphという名前です。
単方向グラフ:Twitter
Twitterでフォロワーを見ると、結果は以下のようになります。
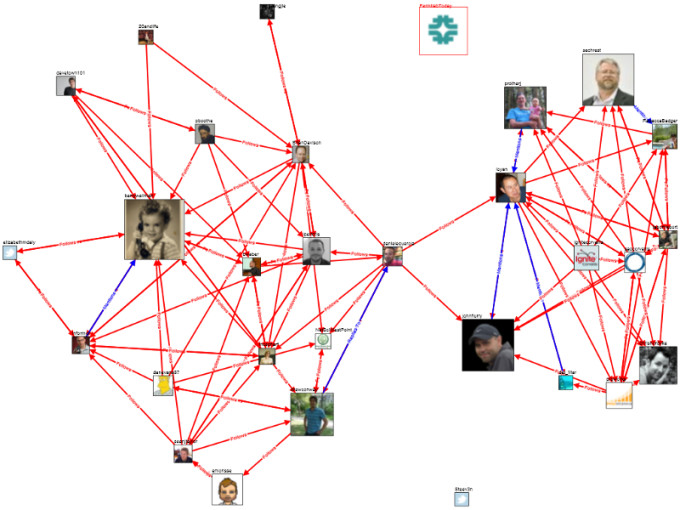
Social Media Research Foundationから引用した画像
この場合、各ノードはTwitterアカウントですが、コネクションは単方向です。これは、例えば私があなたをフォローしても、あなたが私をフォローしてくれるとは限らないからです。
ダイクストラ法アルゴリズム
グラフについて理解したので、最もホットな話題の一つである最短経路問題についてお話しましょう。
この課題は非常に理解しやすいものです。あるグラフの2つのノードについて、あるノードから別のノードへの最短経路(存在する場合)を見つけるという問題です。
私たちにとっては(迷路を解くのと同じくらい)シンプルなゲームですが、機械にとってはできるだけ早く解決しなければならない課題です。
これも、あなたが常に使用しているものです。例えば、Apple Maps Appが最良の経路を計算する方法、またはLinkedInがプロフィールの1次/2次/3次コンタクトを判断する方法について考えてみてください。
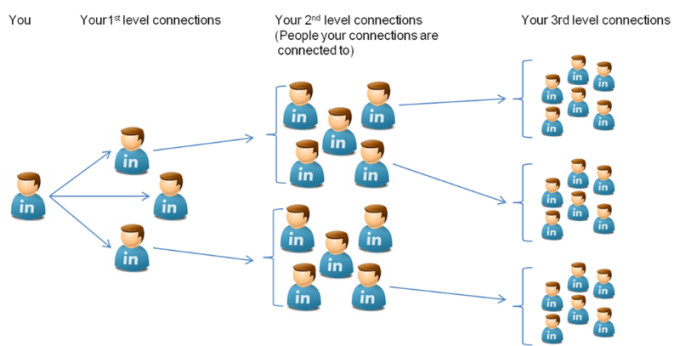
Linkedinから引用した画像
最も有名な最短経路探索アルゴリズムの一つ(あえて言いますが、「最も」有名です)は、ダイクストラ法アルゴリズムで、以下の3つのステップに基づいています。
また到達していない最もコストが低いノードを見つける
そのノードを到達したものとしてマークし、そこからどのノードにアクセスできるかを追跡する
繰り返す
このアルゴリズムは、宛先ノードに到達するか、到達可能なノードがなくなると終了します。
「コストが低い」とは、これまでに通ったすべてのノードから到達するためのコストが低いノードを意味します。
このコストはコネクションに由来します。グラフのコネクションは、同じである場合もありますし(例えばFacebookの友人関係では、あるコネクションと別のコネクションに違いはありません)、異なっている場合もあります。あなたの家に帰るまでの経路が2種類ある場合、ある経路は山か何かを登らなければならないかもしれないため、一つの経路は別の経路より簡単/コストが低いかもしれません。
Swiftのお時間です!
いい感じのスピードで学んでいるので、すべてをSwiftで実装してみましょう!
ノード
| 1 | class Node { |
| 2 | var visited = false |
| 3 | var connections: [Connection] = [] |
| 4 | } |
Nodeクラスは、既に到達したかどうかを確認するためのプロパティ(アルゴリズムによって使用されるもの)と、他のノードへのコネクションの配列にすぎません。
コネクション
| 1 | class Connection { |
| 2 | public let to: Node |
| 3 | public let weight: Int |
| 4 | |
| 5 | public init(to node: Node, weight: Int) { |
| 6 | assert(weight >= 0, "weight has to be equal or greater than zero") |
| 7 | self.to = node |
| 8 | self.weight = weight |
| 9 | } |
| 10 | } |
ノードの定義であったように、各コネクションは特定のノードに割り当てられているため、コネクション自体の中で定義する必要があるのは、その重み(コストとも呼ばれる)とコネクションが連結するノードです。
私は、単方向コネクションを使用しています。この方法を使った方が、双方向グラフと単方向グラフの両方を管理するのが楽です。
道(パス)
最後に、道(パス)を定義する必要があります。道(パス)は、ノードの連続以上のものではありません。
これは、グラフにおいて既に到達した道(パス)と、どのようにそこに到達したのかを追跡するのに役立ちます。
さらに重要なことに、このアルゴリズムは、課題の起点ノードと宛先ノード間の最短経路を記述するために、このエンティティ(実体)を返します。
この定義には、以下のような再帰的な方法を使用します。
| 1 | class Path { |
| 2 | public let cumulativeWeight: Int |
| 3 | public let node: Node |
| 4 | public let previousPath: Path? |
| 5 | |
| 6 | init(to node: Node, via connection: Connection? = nil, previousPath path: Path? = nil) { |
| 7 | if |
| 8 | let previousPath = path, |
| 9 | let viaConnection = connection { |
| 10 | self.cumulativeWeight = viaConnection.weight + previousPath.cumulativeWeight |
| 11 | } else { |
| 12 | self.cumulativeWeight = 0 |
| 13 | } |
| 14 | |
| 15 | self.node = node |
| 16 | self.previousPath = path |
| 17 | } |
| 18 | } |
便宜上、道(パス)のノードに到達するためのコストを追跡するために、cumulativeWeightプロパティを追加しています。このコストは、起点ノードからこのノードに移動したすべてのコネクションの重みの合計です。
アルゴリズム
すべての設定が完了しました!アルゴリズムを掘り下げてみましょう。
| 1 | func shortestPath(source: Node, destination: Node) -> Path? { |
| 2 | var frontier: [Path] = [] { |
| 3 | didSet { frontier.sort { return $0.cumulativeWeight < $1.cumulativeWeight } } // the frontier has to be always ordered |
| 4 | } |
| 5 | |
| 6 | frontier.append(Path(to: source)) // the frontier is made by a path that starts nowhere and ends in the source |
| 7 | |
| 8 | while !frontier.isEmpty { |
| 9 | let cheapestPathInFrontier = frontier.removeFirst() // getting the cheapest path available |
| 10 | guard !cheapestPathInFrontier.node.visited else { continue } // making sure we haven't visited the node already |
| 11 | |
| 12 | if cheapestPathInFrontier.node === destination { |
| 13 | return cheapestPathInFrontier // found the cheapest path |
| 14 | } |
| 15 | |
| 16 | cheapestPathInFrontier.node.visited = true |
| 17 | |
| 18 | for connection in cheapestPathInFrontier.node.connections where !connection.to.visited { // adding new paths to our frontier |
| 19 | frontier.append(Path(to: connection.to, via: connection, previousPath: cheapestPathInFrontier)) |
| 20 | } |
| 21 | } // end while |
| 22 | return nil // we didn't find a path |
| 23 | } |
たった23行のコードです。
最初に、frontierを定義します。frontierとは、これまでに通ったノードから到達できるノードへの道(パス)の集合です。
最初はempty(空)ですが、スクリプトを起動するとすぐに始点ノード(6行目)に道(パス)が追加されます。
ここで、ダイクストラ法アルゴリズムのステップに従いましょう。
1. まだ到達していない最もコストが低いノードを見つける
frontierから最もコストが低い道(パス)を抽出し(9行目)、まだ通っていないノードかどうかを確認し、通っていなかった場合は次のステップ(10行目)に進んでいます。
2. そのノードを到達したものとしてマークし、そこからどのノードにアクセスできるかを追跡する
このステップになるとすぐに、ノードを到達したものとしてマークし(16行目)、ノードのコネクションを調べることによって、このノードから到達可能なすべての新しい(通っていない)ノードを追加します(18~20行目)。
3. 繰り返す
whileサイクルが完了したので、上記の2つのステップを繰り返すだけです!
注1
お気付きかもしれませんが、ステップ1と2の間に何かしています(12~14行目)。
それは、新しい最もコストが低いノードが、宛先ノードであるかどうかを確認することです。もし宛先ノードだった場合は、おめでとうございます!アルゴリズムが完了しました!それ以外の場合は、ステップ2に進みます。
注2
アルゴリズムは、任意の値を返すことがあります(1行目と22行目)。起点ノードと宛先ノードには、相互に連結する道(パス)が存在しない可能性があります。
Swift Playground
OKです!Swiftでダイクストラ法アルゴリズムを使って遊ぶために必要なものをすべて手に入れましたね!以下は、下の方に例が載っているPlaygroundです。
| 1 | class Node { |
| 2 | var visited = false |
| 3 | var connections: [Connection] = [] |
| 4 | } |
| 5 | |
| 6 | class Connection { |
| 7 | public let to: Node |
| 8 | public let weight: Int |
| 9 | |
| 10 | public init(to node: Node, weight: Int) { |
| 11 | assert(weight >= 0, "weight has to be equal or greater than zero") |
| 12 | self.to = node |
| 13 | self.weight = weight |
| 14 | } |
| 15 | } |
| 16 | |
| 17 | class Path { |
| 18 | public let cumulativeWeight: Int |
| 19 | public let node: Node |
| 20 | public let previousPath: Path? |
| 21 | |
| 22 | init(to node: Node, via connection: Connection? = nil, previousPath path: Path? = nil) { |
| 23 | if |
| 24 | let previousPath = path, |
| 25 | let viaConnection = connection { |
| 26 | self.cumulativeWeight = viaConnection.weight + previousPath.cumulativeWeight |
| 27 | } else { |
| 28 | self.cumulativeWeight = 0 |
| 29 | } |
| 30 | |
| 31 | self.node = node |
| 32 | self.previousPath = path |
| 33 | } |
| 34 | } |
| 35 | |
| 36 | extension Path { |
| 37 | var array: [Node] { |
| 38 | var array: [Node] = [self.node] |
| 39 | |
| 40 | var iterativePath = self |
| 41 | while let path = iterativePath.previousPath { |
| 42 | array.append(path.node) |
| 43 | |
| 44 | iterativePath = path |
| 45 | } |
| 46 | |
| 47 | return array |
| 48 | } |
| 49 | } |
| 50 | |
| 51 | func shortestPath(source: Node, destination: Node) -> Path? { |
| 52 | var frontier: [Path] = [] { |
| 53 | didSet { frontier.sort { return $0.cumulativeWeight < $1.cumulativeWeight } } // the frontier has to be always ordered |
| 54 | } |
| 55 | |
| 56 | frontier.append(Path(to: source)) // the frontier is made by a path that starts nowhere and ends in the source |
| 57 | |
| 58 | while !frontier.isEmpty { |
| 59 | let cheapestPathInFrontier = frontier.removeFirst() // getting the cheapest path available |
| 60 | guard !cheapestPathInFrontier.node.visited else { continue } // making sure we haven't visited the node already |
| 61 | |
| 62 | if cheapestPathInFrontier.node === destination { |
| 63 | return cheapestPathInFrontier // found the cheapest path |
| 64 | } |
| 65 | |
| 66 | cheapestPathInFrontier.node.visited = true |
| 67 | |
| 68 | for connection in cheapestPathInFrontier.node.connections where !connection.to.visited { // adding new paths to our frontier |
| 69 | frontier.append(Path(to: connection.to, via: connection, previousPath: cheapestPathInFrontier)) |
| 70 | } |
| 71 | } // end while |
| 72 | return nil // we didn't find a path |
| 73 | } |
| 74 | |
| 75 | // **** EXAMPLE BELOW **** |
| 76 | |
| 77 | class MyNode: Node { |
| 78 | let name: String |
| 79 | |
| 80 | init(name: String) { |
| 81 | self.name = name |
| 82 | super.init() |
| 83 | } |
| 84 | } |
| 85 | |
| 86 | let nodeA = MyNode(name: "A") |
| 87 | let nodeB = MyNode(name: "B") |
| 88 | let nodeC = MyNode(name: "C") |
| 89 | let nodeD = MyNode(name: "D") |
| 90 | let nodeE = MyNode(name: "E") |
| 91 | |
| 92 | nodeA.connections.append(Connection(to: nodeB, weight: 1)) |
| 93 | nodeB.connections.append(Connection(to: nodeC, weight: 3)) |
| 94 | nodeC.connections.append(Connection(to: nodeD, weight: 1)) |
| 95 | nodeB.connections.append(Connection(to: nodeE, weight: 1)) |
| 96 | nodeE.connections.append(Connection(to: nodeC, weight: 1)) |
| 97 | |
| 98 | let sourceNode = nodeA |
| 99 | let destinationNode = nodeD |
| 100 | |
| 101 | var path = shortestPath(source: sourceNode, destination: destinationNode) |
| 102 | |
| 103 | if let succession: [String] = path?.array.reversed().flatMap({ $0 as? MyNode}).map({$0.name}) { |
| 104 | print("Quickest path: \(succession)") |
| 105 | } else { |
| 106 | print("No path between \(sourceNode.name) & \(destinationNode.name)") |
| 107 | } |
結論
学問の世界では、学校のカリキュラムにおいて、グラフ理論が幾何学に取って代わるべきかどうかについての議論があります。コンピュータエンジニアとしては、なぜグラフ理論がこれほど持ち上げられているのかよくわかります。
この記事が皆さんの学びになることを願っています!それでは、また次回お会いしましょう。
注意
一部の読者が、最もコストが低い利用可能な道(パス)を獲得するための最も効率的なアプローチは、frontier配列ではないと指摘してくれました。ソートするのにオーバーヘッドが大きいためです。
確かにそうです。もっと良い方法があります。例えば、Priority Queue(優先度付きキュー)のデータ構造を使用することができます。
サポートしてくださったu/madiyarとIlya Myakotinに感謝申し上げます!
お知らせ!
私のブログがMediumに引っ越ししました!ブログ記事の通知を受け取りたい場合は、こちらからサインアップしてください!ありがとうございます。
Federicoは、バンコク在住のソフトウェアエンジニアであり、Swift、ミニマリズム、設計、iOS開発に対して強い情熱を持っています。
CREDIT:原著者の許諾のもと翻訳・掲載しています。
[原文]Dijkstra’s Algorithm In Swift (Posted Aug 22, 2017) by Federico Zanetello